读书笔记：数学之美-PageRank Google的民主表决式网页排名技术

2017年05月31日 shenbowei

keyword：网页质量衡量，PageRank算法

对于一个特定的查询，搜索结果的排名取决于两组信息：

  • 关于网页的质量信息（Quality）

  • 这个查询与每个网页的相关性信息（Relevance）

本章将介绍衡量网页质量的方法。

PageRank算法原理

Google的PageRank是计算网页自身质量的完美的数学模型，其简单地说就是民主表决。 一个网页的质量是由所有包含它链接的网页共同决定的。 在互联网上，如果一个网页被很多其他网页所链接，说明它受到普遍的承认和信赖，那么它的排名就高。 这就是PageRank的核心思想。 但是，所有网页的表决权是不一样的，即网页排名高的网站的贡献的链接权重理应要大。

网页排名计算
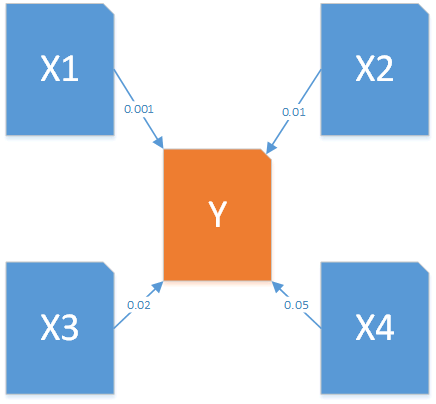
网页排名计算

如上图所示，网页Y的排名来自于所有指向这个网页的其他网页$X_1,X_2,\ldots,X_k$的权重之和。 即网页Y的排名$PageRank=0.001+0.01+0.05+0.02=0.081$。

但是，网页$X_1,X_2,\ldots,X_k$的权重又应该是其自身的网页排名（PageRank）。因此，计算这些网页的排名又会用到更多指向它们的网页的排名， 这就变成了一个怪圈。PageRank算法把这个问题变成了一个二维矩阵相乘的问题，并用迭代的方法解决了这个问题（PageRank的高明之处在于它把互联网当作一个整体来对待）。

  1. 先假设最初所有网页的排名都是相同的，并根据这个初始值算出各个网页的第一次迭代排名。

  2. 然后，根据第一次迭代排名算出第二次的排名（一直迭代下去直至两次迭代差值足够小）。从理论上可以证明无论初始值如何选取，最终算法都能保证网页排名的估计值收敛到真实值。

  • 随着网页数量的增大，这个二维矩阵也变得巨大（元素数量为网页数量的平方），PageRank的发明者佩奇和布林利用稀疏矩阵的计算技巧，大大简化了计算量。

  • 2003年，Google工程师发明了并行计算工具MapReduce，使PageRank的并行计算完全自动化，大大缩短了计算时间。

PageRank的计算方法

假定下面的向量B表示N个网页的排名

矩阵A表示网页之间链接的数目，其中$a_{mn}$代表第$n$个网页指向第$m$个网页的链接数（这里书中写的是$m$指向$n$，个人感觉有问题）

A是已知的，B是未知的，也就是我们需要计算的。

假定$B_i$是第$i$次迭代的结果，那么

初始假设所有网页的排名都是1/N

通过上述的几个公式，我们便可以不断迭代计算出新的$B_i$（计算量很大，因为矩阵A和向量B的数目很大）。 可以证明$B_i$最终会收敛，即$B_i$无限趋近于$B$，此时$B=B \times A$。 因此，当两次迭代结果$B_i$和$B_{i-1}$的差值很小时（可以之前设定个阈值），迭代计算就结束了。 一般来讲，只要10次左右的迭代基本就收敛了。

由于网页之间的链接数量相比互联网的规模非常稀疏（也就是矩阵A中存在大量的0），因此计算网页排名需要对零概率或者小概率事件进行平滑处理。 网页排名是个一维向量，对它的平滑处理只能利用一个小的常熟$\alpha$:

平滑后的$B_i$如上式所示，其中$N$为互联网网页的数量，$\alpha$是一个较小的常熟，$I$为单位矩阵。

网页排名的计算主要是矩阵相乘，这种计算很容易分解成许多小任务，在多台计算上并行处理（MapReduce）。

评论